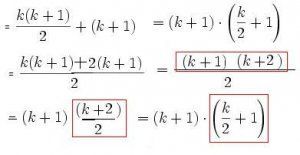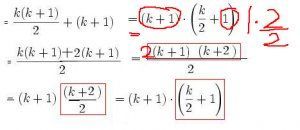Matheproblemchen...

G

Gast7352

Guest

• 19 Apr 2006

• #1

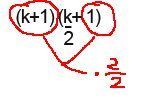
Ok also hab das Problem dass ich nicht so recht schlau werd aus der Gleichung. Hab das aus Wiki so zusammengeflickt, daher das = am Anfang...
Jedenfalls bin ich ziemlich am Ende mit meinen Nerven, kann mir mal jemand erklären, am besten Schritt für Schritt, wie man das löst? Hab ja schon gesucht im Netz, aber die gehen wohl alle davon aus dass jeder sofort sieht wie das umgewandelt wurde.

(Iss ja Mathe und da Computer Rechenmaschienen sind hab ich hier gepostet)
Gruss

 

Anhänge

• 
  Matheproblemchen.JPG

  3,7 KB · Aufrufe: 251

G

Gast7352

Guest

• 19 Apr 2006

• #2

Habs rausgefunden! (3Std aktiv und 6Std passiv etwa...)
Falls andere irgendwann mal das gleiche Prob haben:

 

Anhänge

• 
  Matheproblemlösung.JPG

  12,4 KB · Aufrufe: 250

-T-

Without ME its just AWESO

Dabei seit

12 Jan 2005

Beiträge

368

Reaktionen

42

Ort

Austria

• 19 Apr 2006

• #3

Ist ja ewig her das dich derlei Probleme hatte, aber müsste nicht in der 2ten Zeile auf der rechten Seite:

2(k+1).(k+2)
==========
2


stehen ?
Mfg -T-

 

G

Guest

Sammelaccount

Dabei seit

4 Sep 2001

Beiträge

11.119

Reaktionen

894

• 19 Apr 2006

• #4

Nein, das k(k+1) + 2(k+1) wird ja zu (k+1) (k+2) zusammengefasst.

//edit:

Hm. Irgendwie hast du mich grad unsicher gemacht.

Weil wenn man (k+1)(k+2) auflöst, würde man schließlich auf

k²+3k+2 kommen, was aber nicht dasselbe ist wie k(k+1) + 2(k+1)

//edit2:

Doch, ist dasselbe.

 

Zuletzt bearbeitet: 19 Apr 2006

-T-

Without ME its just AWESO

Dabei seit

12 Jan 2005

Beiträge

368

Reaktionen

42

Ort

Austria

• 19 Apr 2006

• #5

Ich find alles nur dein erstes (grünes) k nicht ?

Edit: wenn du (k +1) durch 2 dividieren willst musst du es ja auch mit 2 multiplizieren ? Sprich auf gleichen Nenner bringen ?

 

Zuletzt bearbeitet: 19 Apr 2006

G

Guest

Sammelaccount

Dabei seit

4 Sep 2001

Beiträge

11.119

Reaktionen

894

• 19 Apr 2006

• #6

Ne, das ist irgend so eine Matheformel D), keine AHnung. Ist bei mir auch schon ne Ecke her.

Die beiden Faktoren, also das erste grüne k und die 2 werden in der Klammer zusammengefasst, da sie beide mit (k+1) multipliziert werden.

Anderes Beispiel wäre: x.(y+5) + z.(y+5) = (y+5) (x+z)

 

-T-

Without ME its just AWESO

Dabei seit

12 Jan 2005

Beiträge

368

Reaktionen

42

Ort

Austria

• 19 Apr 2006

• #7

Nee das versteh ich aber schau dir den rechten Teil der Gleichung nochmal an:
wenn man jetzt alles auf den gleichen Nenner bringt muss man:

 

Anhänge

• 
  k1.jpg

  5,6 KB · Aufrufe: 226

-T-

Without ME its just AWESO

Dabei seit

12 Jan 2005

Beiträge

368

Reaktionen

42

Ort

Austria

• 19 Apr 2006

• #8

und dann kommt man auf :
2(k+1).(k+2)
(durch 2)

 

G

Guest

Sammelaccount

Dabei seit

4 Sep 2001

Beiträge

11.119

Reaktionen

894

• 19 Apr 2006

• #9

Der Nenner steht doch schon bei beiden. Also braucht man sie doch garnicht gleichnamig machen.
Steht doch unter dem gesamten Ausdruck
_
2

 

-T-

Without ME its just AWESO

Dabei seit

12 Jan 2005

Beiträge

368

Reaktionen

42

Ort

Austria

• 19 Apr 2006

• #10

rechte seite !!!

 

G

Gast7352

Guest

• 19 Apr 2006

• #11

Ha geil Jungs!
Das Problem bestand bei der "Vollständigen Induktion".
http://de.wikipedia.org/wiki/Vollständige_Induktion
Dort ist die Formel, wie ich sie beim ersten Post verlinkt habe.

 

G

Guest

Sammelaccount

Dabei seit

4 Sep 2001

Beiträge

11.119

Reaktionen

894

• 19 Apr 2006

• #12

oO

Also das bei wiki ist mir zu hoch!

@ -T-

Jetzt weiß ich, warum wir aneinander vorbeireden.

Du hast geschrieben

aber müsste nicht in der 2ten Zeile auf der rechten Seite:

Zum Vergrößern anklicken....

Ich hab das auf die Grafik bezogen. Du meinst aber die unterste (also in der Grafik die 3.) Zeile, oder?

 

-T-

Without ME its just AWESO

Dabei seit

12 Jan 2005

Beiträge

368

Reaktionen

42

Ort

Austria

• 19 Apr 2006

• #13

ich meinte:

 

Anhänge

• 
  Matheproblemlösung.jpg

  20,5 KB · Aufrufe: 178

G

Gast7352

Guest

• 19 Apr 2006

• #14

Madman schrieb:

oO

Also das bei wiki ist mir zu hoch!

Zum Vergrößern anklicken....

Da hast du recht, ich habs ja nicht durch deren Erklärungen verstanden. Die machen alles so endlos superkorrekt und hyperkompliziert...also zum Glück gibts noch andere Quellen auf normaldeutsch.
(Manchmal aber passts schon )

 

G

Guest

Sammelaccount

Dabei seit

4 Sep 2001

Beiträge

11.119

Reaktionen

894

• 19 Apr 2006

• #15

@ -T-

Ach so, verstehe.

Aber an dieser Stelle braucht man nicht mit 2/2 zu multiplizieren. 1 = 2/2, demzufolge kann man es einfach dadurch ersetzen.

Somit hat man dann

k.......2.......k + 2
-...+..-...=..------
2.......2.........2

Der erste Faktor (also (k+1)) brauch ja nicht gleichnamig gemacht werden, da er multipliziert wird, demzufolge hat man dann:

(k+1)(k+2)
----------
......2

 

Zuletzt bearbeitet: 19 Apr 2006

-T-

Without ME its just AWESO

Dabei seit

12 Jan 2005

Beiträge

368

Reaktionen

42

Ort

Austria

• 19 Apr 2006

• #16

da er multipliziert

Zum Vergrößern anklicken....

ach du s.hit...
hab mich so darin verbissen das ich schon garnicht mehr gesehen hab das es nicht addiert wird...
nagut haste recht,
und jetz zu was anderm
Mfg -T-

 

G

Guest

Sammelaccount

Dabei seit

4 Sep 2001

Beiträge

11.119

Reaktionen

894

• 19 Apr 2006

• #17

Boah, bin ich noch gut!

 

D

Dewitt

Power-User

Dabei seit

2 Feb 2004

Beiträge

1.470

Reaktionen

106

• 19 Apr 2006

• #18

Ähh, Leute....ihr denkt viel zu kompliziert.

1) Auf der rechten Seite steht doch nicht anderes als

k/2 mal (k+1) + 1 mal (k+1) (Ich habe hier bewusst "mal" geschrieben, damit man sieht wo sich das jeweilige Produkt befindet. Außerdem den Bruch etwas geordnet und mit 1 erweitert.)

2) Man klammert (k+1) aus. (Hierbei kann man das (k+1) auch durch z.B. a ersetzen, damit´s einfacher geht.)
Also steht da:

(k/2 + 1) mal (k+1)

Und das ist doch nichts anderes, als die linke Seite.

 

G

Guest

Sammelaccount

Dabei seit

4 Sep 2001

Beiträge

11.119

Reaktionen

894

• 19 Apr 2006

• #19

Das hab ich doch hier im Post 4 schon geschrieben.

 

D

Dewitt

Power-User

Dabei seit

2 Feb 2004

Beiträge

1.470

Reaktionen

106

• 19 Apr 2006

• #20

Upps, hast recht. Das sah mir aber auch schon zu kompliziert aus beim "Drüberfliegen". Hamma halt beide rischtisch gedacht, gelle?